|
Be the first user to complete this post
|
Add to List |
310. Dijkstra’s – Shortest Path Algorithm (SPT) – Adjacency List and Min Heap
Earlier we have seen the basics of Dijkstra algorithm. In this article, we will see its implementation using the adjacency list and Min Heap.
brief: What is Dijkstra’s algorithm?
- Dijkstra algorithm is a greedy algorithm.
- It finds a shortest path tree for a weighted undirected graph.
- This means it finds the shortest paths between nodes in a graph, which may represent, for example, road networks
- For a given source node in the graph, the algorithm finds the shortest path between the source node and every other node.
- This algorithm is also used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined.
- Dijkstra’s algorithm is very similar to Prim’s algorithm. In Prim’s algorithm, we create minimum spanning tree (MST) and in the Dijkstra algorithm, we create a shortest-path tree (SPT) from the given source.
We strongly recommend reading the following articles
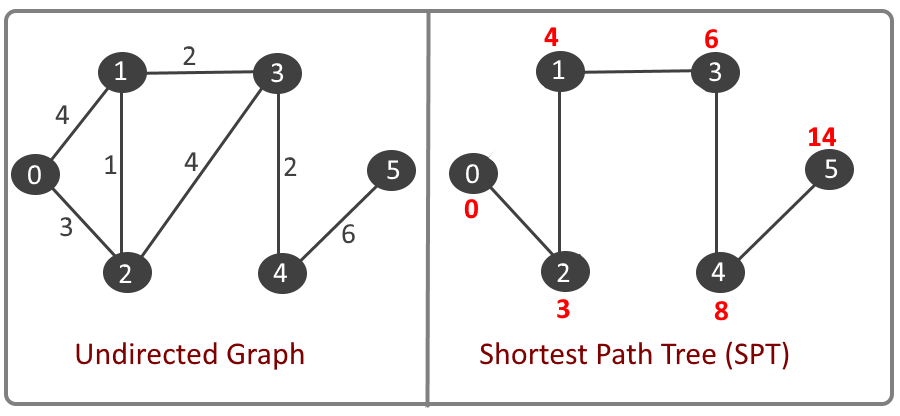
Example:
Implementation – Adjacency List and Min Heap
- Create min Heap of size = no of vertices.
- Create a heapNode for each vertex which will store two pieces of information. a). vertex b). Distance from vertex from source vertex.
- Use spt[] to keep track of the vertices which are currently in min-heap.
- For each heapNode, initialize distance as +∞ except the heapNode for the source vertex for which distance will be 0.
- while minHeap is not empty
- Extract the min node from the heap, say it vertex u, and add it to the SPT.
- Decrease distance: For adjacent vertex v, if v is not in SPT[] and distance[v] > distance[u] + edge u-v weight then update distance[v] = distance[u] + edge u-v weight
Time Complexity:
Total vertices: V, Total Edges : E
- O(logV) – to extract each vertex from the heap. So for V vertices – O(VlogV)
- O(logV) – each time decreases the distance of a vertex. Decrease distance will be called for at most once for each edge. So for total E edge – O(ElogV)
- So overall complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)
See the animation below for more understanding
Complete Code:
Output:
Dijkstra Algorithm: (Adjacency List + Min Heap) Source Vertex: 0 to vertex 0 distance: 0 Source Vertex: 0 to vertex 1 distance: 4 Source Vertex: 0 to vertex 2 distance: 3 Source Vertex: 0 to vertex 3 distance: 6 Source Vertex: 0 to vertex 4 distance: 8 Source Vertex: 0 to vertex 5 distance: 14

