|
This post is completed by 1 user
|
Add to List |
417. Maximum number edges to make Acyclic Undirected/Directed Graph
Given- Given V vertices, what is the maximum number of edges can be added to make Acyclic Undirected Graph. Follow up - what is the maximum number of edges that can be added to make Acyclic Directed Graph.
Example:
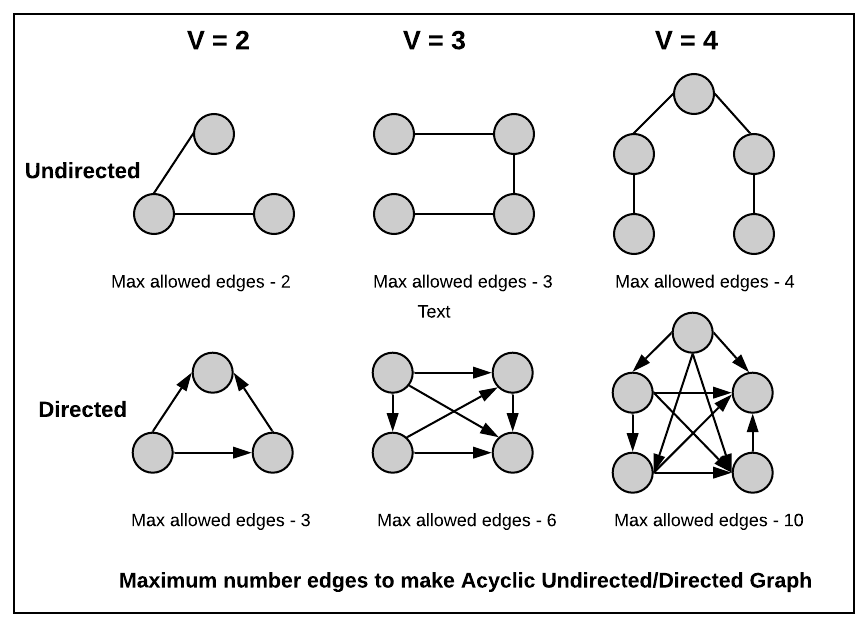
Approach:
For Undirected Graph - It will be a spanning tree (read about spanning tree) where all the nodes are connected with no cycles and adding one more edge will form a cycle. In the spanning tree, there are V-1 edges.
For Directed Graph - Construct the graph similar to topological order (Read about topological order - where all the edges go to one direction and there will not be any circular dependency, means there is no cycle). Take the first vertex and have a directed edge to all the other vertices, so V-1 edges, second vertex to have a directed edge to rest of the vertices so V-2 edges, third vertex to have a directed edge to rest of the vertices so V-3 edges, and so on. This will construct a graph where all the edges in one direction and adding one more edge will produce a cycle.
So the total number of edges = (V-1) + (V-2) + (V-3) +---------+2+1 = V(V-1)/2. (sum of first N natural numbers is N(N+1)/2)
Output:
Maximum edges to make Acyclic Undirected Graph with 3 vertices are: 2 Maximum edges to make Acyclic Directed Graph with 3 vertices are: 3 --------------------------------- Maximum edges to make Acyclic Undirected Graph with 4 vertices are: 3 Maximum edges to make Acyclic Directed Graph with 4 vertices are: 6 --------------------------------- Maximum edges to make Acyclic Undirected Graph with 5 vertices are: 4 Maximum edges to make Acyclic Directed Graph with 5 vertices are: 10

